7 algoritmi, kas jāzina katram programmētājam

Kā programmēšanas students jūs, iespējams, savas karjeras laikā esat iemācījušies daudz dažādu algoritmu. Jebkuram programmētājam ir absolūti nepieciešama prasme apgūt dažādus algoritmus.

Izmantojot tik daudz algoritmu, var būt grūti izsekot būtiskajam. Ja jūs gatavojaties intervijai vai vienkārši papildināt savas prasmes, šis saraksts padarīs to salīdzinoši vienkāršu. Lasiet tālāk, kad mēs uzskaitām programmētājiem vissvarīgākos algoritmus.

1. Dijkstra algoritms

Edgers Dijkstra bija viens no sava laika ietekmīgākajiem datorzinātniekiem, un viņš tajā piedalījās daudzas dažādas skaitļošanas zinātnes jomas, ieskaitot operētājsistēmas, kompilatora uzbūvi un daudz ko citu vairāk. Viens no ievērojamākajiem Dijkstra ieguldījumiem ir viņa īsākā ceļa grafika algoritma atjautība, kas pazīstama arī kā Dijkstra īsākā ceļa algoritms.

Dijkstra algoritms atrod vienu īsāko ceļu grafikā no avota līdz visām grafika virsotnēm. Katrā algoritma atkārtojumā tiek pievienota virsotne ar minimālo attālumu no avota un tāda, kas nepastāv pašreizējā īsākajā ceļā. Šis ir mantkārīgais īpašums, ko izmanto Džikstras algoritms.

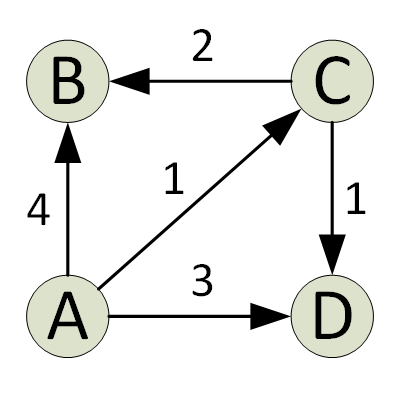
Algoritms parasti tiek īstenots, izmantojot kopu. Dijkstra algoritms ir ļoti efektīvs, ja to īsteno ar Min Heap; īsāko ceļu var atrast tikai O (V+ElogV) laikā (V ir virsotņu skaits un E ir malu skaits noteiktā grafikā).

Dijkstra algoritmam ir savi ierobežojumi; tas darbojas tikai uz virzītiem un nevirzītiem grafikiem ar pozitīva svara malām. Negatīviem svariem parasti ieteicams izmantot Belmana-Forda algoritmu.

Intervijas jautājumi parasti ietver Djikstra algoritmu, tāpēc mēs ļoti iesakām izprast tā sarežģīto informāciju un pielietojumu.

2. Apvienot Kārtot

Šajā sarakstā ir daži šķirošanas algoritmi, un apvienošanas kārtošana ir viens no vissvarīgākajiem algoritmiem. Tas ir efektīvs šķirošanas algoritms, kura pamatā ir sadalīšanas un iekarošanas programmēšanas tehnika. Sliktākajā gadījumā apvienošanas kārtošana var sakārtot “n” skaitļus tikai O (nlogn) laikā. Salīdzinot ar primitīvām šķirošanas metodēm, piemēram Burbuļu kārtošana (tas prasa O (n^2) laiku), sapludināšanas kārtošana ir izcili efektīva.

Saistīts: Ievads apvienošanas kārtošanas algoritmā

Apvienojot kārtošanu, sakārtojamais masīvs tiek atkārtoti sadalīts apakšmasos, līdz katrs apakšmasīts sastāv no viena numura. Pēc tam rekursīvs algoritms atkārtoti apvieno apakšmasas un kārto masīvu.

3. Ātrsortēšana

Quicksort ir vēl viens šķirošanas algoritms, kura pamatā ir sadalīšanas un iekarošanas programmēšanas tehnika. Šajā algoritmā vispirms tiek izvēlēts elements kā šarnīrsavienojums, un pēc tam viss masīvs tiek sadalīts ap šo šarnīru.

Kā jūs droši vien uzminējāt, efektīvai kārtošanai izšķiroša nozīme ir labam pagrieziena punktam. Šarnīrsavienojums var būt nejaušs elements, multivides elements, pirmais elements vai pat pēdējais elements.

Ātrās šķirošanas ieviešana bieži atšķiras ar to, kā tiek izvēlēts šarnīrsavienojums. Vidējā gadījumā ātrā šķirošana sakārtos lielu masīvu ar labu pagriezienu tikai O (nlogn) laikā.

Vispārējais ātrās šķirošanas pseidokods atkārtoti sadala masīvu šarnīrā un pozicionē to pareizajā apakšslāņa pozīcijā. Tas arī novieto elementus, kas ir mazāki par pagriezienu pa kreisi, un elementus, kas ir lielāki par pagriezienu pa labi.

4. Dziļuma pirmā meklēšana

Dziļuma pirmā meklēšana (DFS) ir viens no pirmajiem grafiku algoritmiem, ko māca studentiem. DFS ir efektīvs algoritms, ko izmanto grafika pārvietošanai vai meklēšanai. To var arī pārveidot, lai to izmantotu koku šķērsošanā.

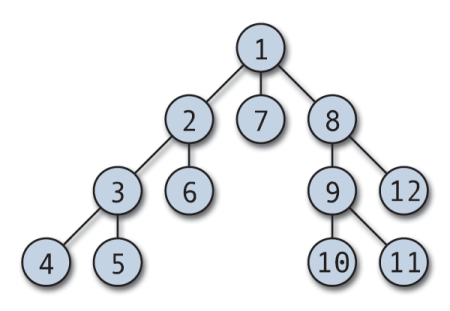
DFS šķērsošanu var sākt no jebkura patvaļīga mezgla, un tas ienirst katrā blakus esošajā virsotnē. Algoritms atgriežas, ja nav neapmeklētas virsotnes vai ir strupceļš. DFS parasti tiek ieviests ar kaudzīti un Būla masīvu, lai izsekotu apmeklētajiem mezgliem. DFS ir vienkārši ieviešams un ārkārtīgi efektīvs; tas darbojas (V+E), kur V ir virsotņu skaits un E ir malu skaits.

Tipiski DFS šķērsošanas lietojumi ietver topoloģisko kārtošanu, ciklu noteikšanu grafikā, ceļa meklēšanu un cieši saistītu komponentu atrašanu.

5. Platuma pirmā meklēšana

Platuma pirmā meklēšana (BFS) ir pazīstama arī kā līmeņa pasūtījumu šķērsošana kokiem. BFS darbojas O (V+E) līdzīgi kā DFS algoritms. Tomēr BFS kaudzes vietā izmanto rindu. DFS ienirst grafikā, bet BFS šķērso grafiku platumā.

BFS algoritms izmanto rindu, lai izsekotu virsotnēm. Neapmeklētās blakus esošās virsotnes tiek apmeklētas, iezīmētas un ievietotas rindā. Ja virsotnei nav blakus esošas virsotnes, tad virsotne tiek noņemta no rindas un izpētīta.

BFS parasti izmanto vienādranga tīklos, īsākajā nesvērtā grafika ceļā un minimālā aptverošā koka atrašanai.

6. Binārā meklēšana

Binārā meklēšana ir vienkāršs algoritms vajadzīgā elementa atrašanai sakārtotā masīvā. Tas darbojas, atkārtoti sadalot masīvu uz pusēm. Ja nepieciešamais elements ir mazāks par vidējo elementu, tad vidējā elementa kreisā puse tiek apstrādāta tālāk; pretējā gadījumā labā puse tiek uz pusi samazināta un tiek pārmeklēta vēlreiz. Procesu atkārto, līdz tiek atrasts nepieciešamais elements.

Sliktākā binārās meklēšanas laika sarežģītība ir O (logn), kas padara to ļoti efektīvu lineāro masīvu meklēšanā.

7. Minimālie aptverošā koka algoritmi

Diagrammas minimālajam aptverošajam kokam (MST) ir minimālās izmaksas starp visiem iespējamajiem aptverošajiem kokiem. Stiepjoša koka izmaksas ir atkarīgas no tā malu svara. Ir svarīgi atzīmēt, ka var būt vairāk nekā viens minimālais aptverošais koks. Ir divi galvenie MST algoritmi, proti, Kruskal un Prim.

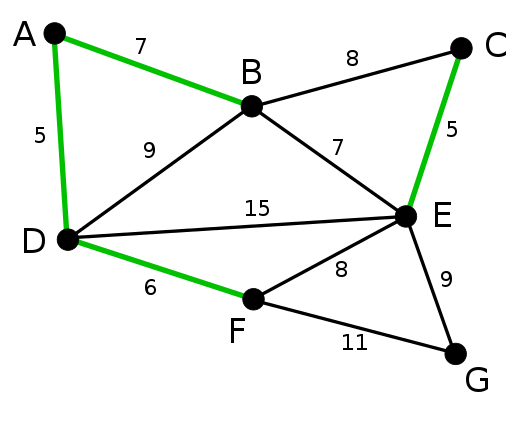
Kruskal algoritms izveido MST, pievienojot augošajam komplektam malu ar minimālām izmaksām. Algoritms vispirms kārto malas pēc to svara un pēc tam pievieno malas MST, sākot no minimālā.

Ir svarīgi atzīmēt, ka algoritms nepievieno malas, kas veido ciklu. Retiem grafikiem priekšroka tiek dota Kruskal algoritmam.

Prim algoritms izmanto arī mantkārīgu īpašumu un ir ideāli piemērots blīvām diagrammām. Prim MST galvenā ideja ir divas atšķirīgas virsotņu kopas; vienā komplektā ir augošais MST, bet otrā - neizmantotās virsotnes. Katrā atkārtojumā tiek izvēlēta minimālā svara mala, kas savienos abas kopas.

Minimālie aptverošo koku algoritmi ir būtiski klasteru analīzei, taksonomijai un apraides tīkliem.

Efektīvs programmētājs pārzina algoritmus

Programmētāji nepārtraukti mācās un attīsta savas prasmes, un ir dažas būtiskas lietas, kas jāapgūst ikvienam. Prasmīgs programmētājs zina dažādus algoritmus, katra priekšrocības un trūkumus un to, kurš algoritms būtu vispiemērotākais konkrētajam scenārijam.

Ievads čaulas kārtošanas algoritmā

Kaut arī čaumalu kārtošana nav visefektīvākā metode, iesācējiem ir daudz ko gūt, to praktizējot.

Lasīt Tālāk

Par autoru